Optimizing Lens Systems for Tolerance Desensitization

When designing a lens system, the optical designer typically seeks to minimize the overall cost to meet a given set of specifications. The designer must consider not only the nominal design performance, but also the effects of fabrication tolerances, alignment errors and compensation methods that have an impact on the final “as-built” performance. Systems requiring tight tolerances or complicated compensation strategies in order to meet the performance specifications will generally be more expensive to manufacture and more complicated to assemble. Ideally, the designer will produce a design form that meets as-built performance goals and is naturally less sensitive to fabrication and alignment errors.

There are a number of published methods for desensitizing a lens as part of the optimization process. Many of these methods apply optimization constraints that indirectly control system sensitivity. The indirect approaches can be effective, but do not directly correlate to typical performance specifications (such as RMS wavefront error). These methods also generally do not include the impact of tolerance compensators. There are other, more direct approaches to tolerance desensitization such as creating additional perturbed configurations and optimizing the nominal and perturbed configurations simultaneously, but the setup for these approaches can be complicated, and the optimization run times can be long.

Synopsys’ CODE V optical design software package includes an optional, separate error function based on estimated as-built performance. The approach uses CODE V’s fast wavefront differential tolerancing algorithm, and allows direct optimization of as-built RMS wavefront performance, including the impact of all supported tolerance types (such as decenter, tilt, wedge, thickness, curvature, aspheric errors, refractive index errors, etc.), as well as realistic compensation using one or many supported compensators (such as defocus, element decenter, airspace adjustment, etc.).

Designing a cell phone camera lens

As an example, let’s consider an injection-molded lens for a cell phone camera. Over a billion mobile phone camera lenses are produced each year. Small improvements in production yields have the potential to reap significant cost savings!

The starting system is a 4.53 mm, ƒ/2.8 lens with a 66⁰ full field of view. It consists of four elements in which every surface is a 12^th to 14^th order asphere, and a cover plate.

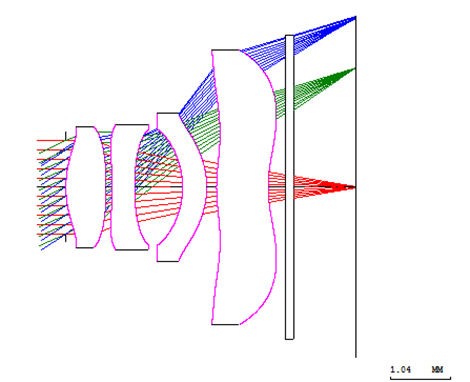
Figure 1: Cell phone camera lens starting system

If we optimize the system for the best nominal RMS wavefront error performance, without regard to tolerance sensitivity, we get the following form (note that for optimization, 13 field points were used, and this was reduced to 7 field points for analysis):

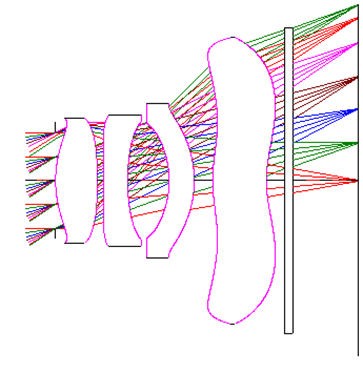
Figure 2: Cell phone lens optimized for best nominal performance

We now apply typical fabrication and assembly tolerances for small molded optics as given in Table 1.

Table 1: Typical tolerances for molded plastic/glass cell phone assemblies

With these tolerances, and a defocus compensator, we can analyze the probability of achieving a certain RMS wavefront error performance at each field, and display the results on a cumulative probability chart:

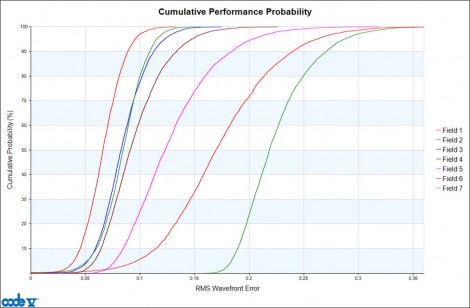
Figure 3: Cumulative probability estimates for as-built RMS wavefront error at seven fields for cell phone lens optimized for best nominal performance

Per Figure 3, for field 1 (on-axis), 80% of built systems are likely to have an RMS wavefront error performance of approximately 0.078 waves RMS or better. For field 7 (the outermost field), 80% of systems are likely to have a performance of 0.25 waves RMS, or better, and 20% of built systems are likely to be worse. As estimated as-built performance improves, these curves will move towards the left side of the chart.

Relative weighting

To include the as-built performance error function component in optimization, we use the same set of optimization inputs with the addition of one extra input: the relative weighting of the as-built error function component to the other error function components. An independent weighting can be applied as a function of field position and zoom configuration, in order to balance the optimized as-built performance, if desired. The resulting lens form optimized with the as-built performance error function is shown in Figure 4, and does not appear signficantly different than before.

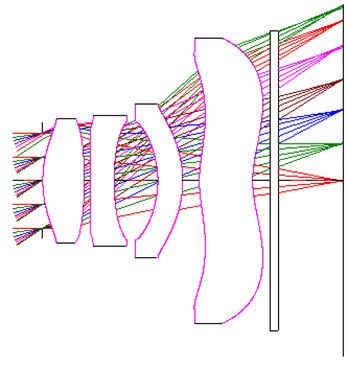
Figure 4: Cell phone lens locally optimized including as-built performance error function

However, the cumulative probability performance plots show that on average, the curves have moved towards the left, indicating reduced tolerance sensitivity:

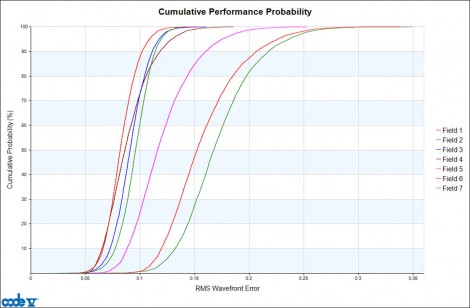
Figure 5: Cumulative probability estimates for as-built RMS wavefront error at seven fields for cell phone lens locally optimized including as-built performance error function

If we analyze the average performance over the field at the 97.7% (Mean + 2σ) probability, we find that for this design, the as-built performance improved by 11%.

The optimization of tolerance insensitive design forms can also be used with global optimization algorithms. For example, the field averaged as-built performance at the 97.7% cumulative probability for the best system found with CODE V’s Global Synthesis optimization method is 24% better than the design form optimized without regard to tolerance desensitization.

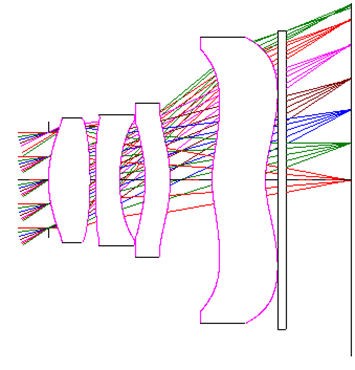
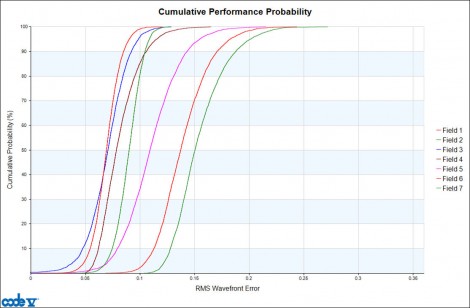
Figure 6: Lens cross-section and cumulative probability estimates for as-built RMS wavefront error at seven fields for best globally optimized solution,  including the as-built performance error function

The ability to easily incorporate tolerance desensitization in optimization on a direct performance metric such as RMS wavefront error, including the realistic modeling of compensation, greatly extends the optical designer’s ability to produce designs that meet as-built performance specifications at a minimized cost.

Written by David Hasenauer, the CODE V Product Manager in the Optical Solutions Group at Synopsys, Inc. (formerly Optical Research Associates, ORA) based in Mountain View, California (US).